Table of Contents
本篇文章針對不同軸向有不同層數的方塊設計,不過只適用在至少兩個軸向層數相同的方塊(EX:2X2X3、3X3X2、4X4X5、4X4X6以此類推),三個軸向皆不同層數的方塊(EX:3X4X5)並不完全適用。

首先我們要從2X2X3 3X3X2開始講(因為是自己手工製作的所以比較簡陋……)
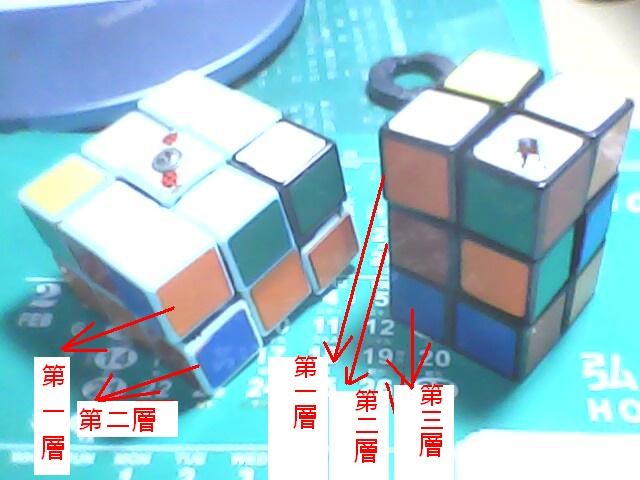
先洗亂……並且以你的智慧把第一層拼好(因為結構限制,側面轉的時候每次轉都要轉180度)

223不等階魔術方塊
都完成後我們先從2X2X3開始(第二層可以先不管 先做第三層)
2X2X3的狀況較單純,第三層只需要換角(因為根本沒有邊…)。

以下圖那面朝自己並以箭頭方向為第一步做公式(R2 U R2 U R2 U2 R2 F2 U2 F2 U F2 U F2 U’)

如果遇到對角線上的角錯位時,只須要做兩次上述公式就可以復原了。
完成後:
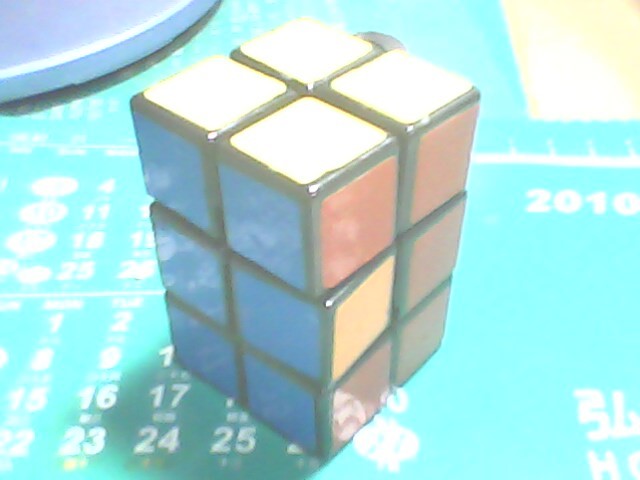
接著用(R2 U2)*3把第二層轉回來就完成了

332不等階
至於3X3X2一樣先做換角公式,把角塊復原,……換好後如下


接下來我們要做的是換邊 依上圖的狀況要先換這兩個
以下圖那面朝自己做公式(R2 D’ F2 [R2 U2]3 F2 D R2)

完成後如下圖,接著請用你對3X3X3的了解把它解完(簡單的對邊互換),一樣因為結構限制,部分轉向只能一次轉180度。



我們的3X3X2 2X2X3都完成了 接著我們來看3X3X4 3X3X5 3X3X7吧

334不等階
解這類的方塊一般我們都從外層開始解
首先我們來看3X3X4 先用3X3X2的方法解出外層

接著,因為內層沒有頂、底面的顏色,所以要自己假設,初學者在假設時因為不習慣容易出錯,建議放慢腳步多思考多觀察。

接著一樣以3X3X2的方式解

這是內層第一層解完的樣子

有時解完時會遇到特殊狀況如上,接著,將方塊互換成下圖(重複右邊內層180頂層180三次即可。)

接著做公式 ※符號加上( )轉內層 [ ]內外一起轉
{[R]2 D2 U3 (R)2 U2 D2 [R]2}就完成了

335不等階

3X3X5的話可以用3X3X3的方法先解外層比較快

接著再以3X3X4的方法解內層就完成了

至於3X3X7做兩次內層即可